Chapter 6 Continuous Probability Distributions

D cannot be used to approximate discrete probability distributions 2. It is measured on a continuous interval or ratio scale.

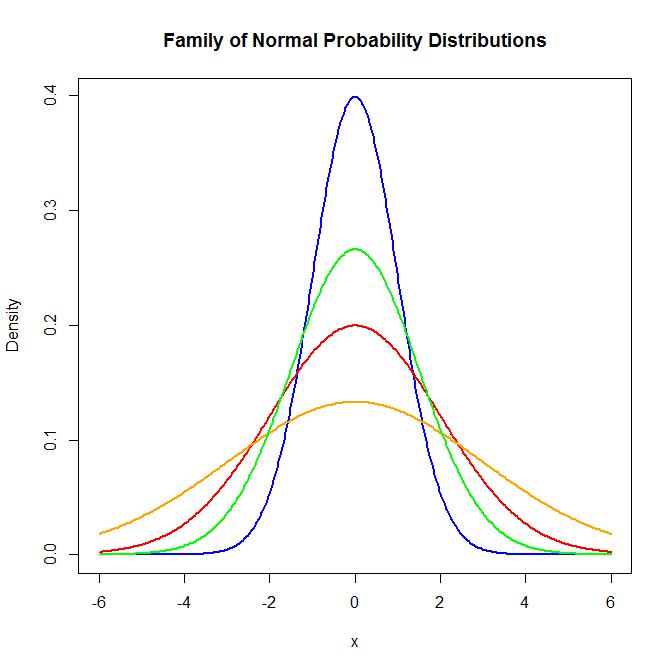
Continuous Probability Distributions Env710 Statistics Review Website

In Chapters 4 and 5 the focus was on probability distributions for a single random variable.

. If we discretize X by measuring depth to the nearest meter then possible values are nonnegative integers less. Let U Uniform01 and F be a CDF. Continuous Improvement Toolkit.

Study with Quizlet and memorize flashcards containing terms like 1. In its standardized form the normal distribution a has a mean of 0 and a standard deviation of 1. A set of real numbers a set of vectors a set of arbitrary non-numerical values etcFor example the sample space of a coin flip would be.

R has built-in functions for working with normal distributions and normal random variables. P x x P Xx For all x belongs to the range of X. Chapters 1 and 2 deal with basic ideas of probability theory.

The Probability Mass Function PMF is also called a probability function or frequency function which characterizes the distribution of a discrete random variable. Assuming that the coin is fair we have Then The probability function is thus given by Table 2-2. 1232 Generating Continuous Probability Distributions from the Uniform Distribution- Inverse Transformation Method At least in principle there is a way to convert a uniform distribution to any other distribution.

We also introduce the q prefix here which indicates the inverse of the cdf function. Chapter 6 deals with probability distributions. Lets see how we can do this.

Schaums Outline of Probability and Statistics CHAPTER 2 Random Variables and Probability Distributions 35 EXAMPLE 22 Find the probability function corresponding to the random variable X of Example 21. It is noted that the probability function should. P1 or more accidents 1 P 0.

An experi-ment whose outcome cannot be determined in advance but is nevertheless still. In this distribution the set of possible outcomes can take on values in a continuous range. In other words what is the probability of 1 or more accidents taking place.

Mostly that chapter focused on the binomial experiment. 4 Probability Distributions for Continuous Variables Suppose the variable X of interest is the depth of a lake at a randomly chosen point on the surface. Chapter 1 Random Experiments and Probability Models 11 Random Experiments The basic notion in probability is that of a random experiment.

For different values of the random variable we can find its respective probability. PX 0 PTT 1 4 PX 1 PHT. What is the probability of at least 1 accident taking place in a given week.

441 Computations with normal random variables. In Chapter 1 an axiomatic framework is presented while in Chapter 2 the important concept of a random vari-able is introduced. Can assume an infinite number of values within a given range.

We can add the probabilities above 0 or use the complement method. Continuous Probability Distributions Chapter 5 dealt with probability distributions arising from discrete random variables. The root name for these functions is norm and as with other distributions the prefixes d p and r specify the pdf cdf or random sampling.

The cumulative probability distribution is also known as a continuous probability distribution. There are many other experiments from discrete random variables that exist but are not covered in this book. Let M the maximum depth in meters so that any number in the interval 0 M is a possible value of X.

For any event of a random experiment we can find its corresponding probability. C has an area equal to 05. Are some of the continuous random variables.

Which of the following about the normal distribution is not true. The times of commercial flights between Atlanta and Los Angeles are 467 hours 513 hours and so on. Section 261 gives a simple derivation of the joint distribution of the sample mean and sample variance of a normal data sample.

Also assume F is continuous and strictly increasing as a. Let X be a discrete random variable of a function then the probability mass function of a random variable X is given by. B has a mean of 1 and a variance of 0.

For example a set of real numbers is a continuous or normal distribution as it gives all the possible outcomes of real numbers. The height weight age of a person the distance between two cities etc. As another reminder a probability distribution has an associated function f that is referred to as a probability mass function PMF or probability distribution function PDF.

For example in Chapter 4 the number of successes in a Binomial experiment was explored and in Chapter 5 several popular distributions for a continuous random variable were considered. 26 Some Important Continuous Distributions. For discrete random variables the PMF is a function from Sto the interval 01 that associates a probability with each x2S ie fx PX x.

6 A 15-hour run at 105 percent rated maximum continuous power with 105 percent maximum continuous speed or at full throttle and corresponding speed at standard sea level carburetor entrance pressure if 105 percent of the rated maximum continuous power is not exceeded. The random variable is the time in hours and is measured on a continuous scale of time. A probability distribution is a mathematical description of the probabilities of events subsets of the sample spaceThe sample space often denoted by is the set of all possible outcomes of a random phenomenon being observed.

Chi-Square and ANOVA Tests. It may be any set.

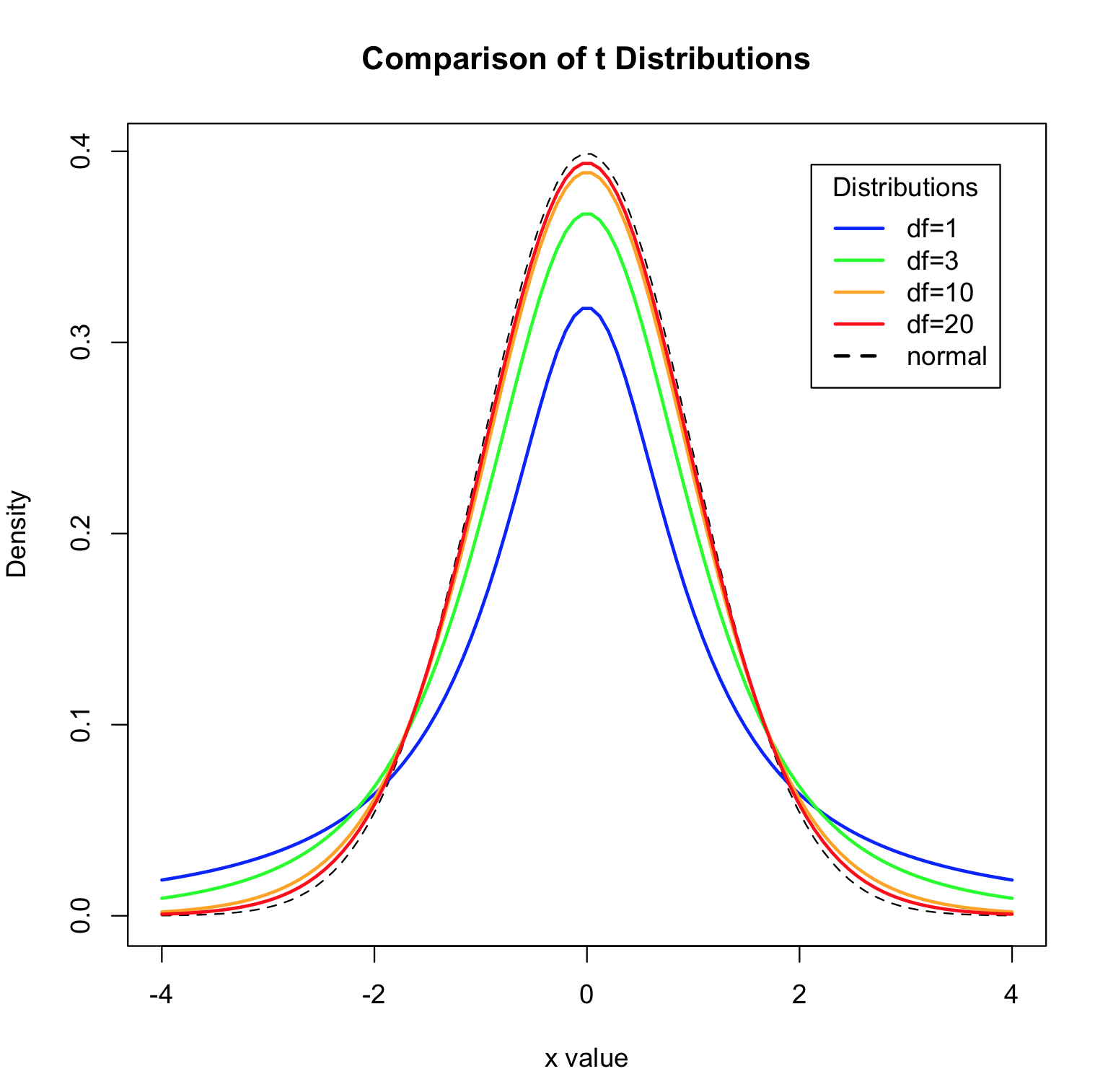
Continuous Probability Distributions Env710 Statistics Review Website

Continuous Probability Distribution An Overview Sciencedirect Topics

Stat 2040 Chapter 6 Continuous Random Variables And Continuous Probabil Oneclass

Chapter 6 Continuous Random Variables And The Normal Distribution Prem Mann Introductory Statistics 8 E Copyri Probability Math Anxiety Sampling Distribution